Henry Pitot (1695-1771), ingeniero y físico francés. Fue militar, estudió matemáticas en forma autodidacta. Algunos de sus aportes son el invento del “tubo de Pitot” que es un instrumento destinado, entre otras aplicaciones, a la medición del caudal a través de la cuantificación de la velocidad del flujo y que utilizó para medir el caudal del Sena.
Teorema de Pitot
El teorema de Pitot es un resultado geométrico fascinante que involucra a los cuadriláteros cíclicos, es decir, aquellos que pueden ser inscritos en una circunferencia. Este teorema, nombrado en honor al físico Henri Pitot, establece una interesante relación entre las longitudes de los lados de un cuadrilátero cíclico.
Consideremos un cuadrilátero ABCD circunscrito a una circunferencia, con vértices A, B, C y D. El teorema de Pitot establece que la suma de las longitudes de los lados opuestos de este cuadrilátero es igual a la suma de las longitudes de los lados adyacentes. En términos matemáticos, el teorema se expresa como:

Este resultado es notable porque establece una conexión entre los lados de un cuadrilátero circunscrito a una circunferencia, independientemente de la forma específica del cuadrilátero. En otras palabras, la suma de las longitudes de los lados opuestos es constante para cualquier cuadrilátero cíclico.
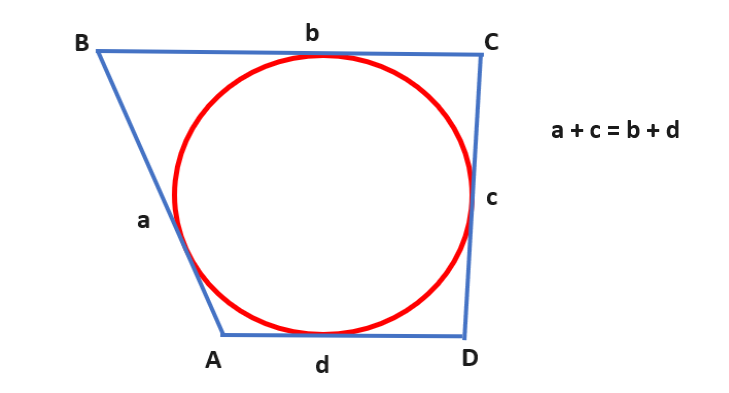
La demostración de este teorema implica el uso de propiedades geométricas de los ángulos en la circunferencia y se basa en conceptos fundamentales de la geometría euclidiana. Al explorar la relación entre las longitudes de los lados de un cuadrilátero inscrito, el teorema de Pitot ofrece una perspectiva única sobre las propiedades de estas figuras geométricas especiales.
En resumen, el teorema de Pitot proporciona una elegante conexión entre los lados de un cuadrilátero circunscrito a una circunferencia, mostrando la riqueza de las relaciones que pueden descubrirse en la geometría euclidiana.
Atte. Patricio Figueroa M – Profesor de Matemáticas








