En la enseñanza de las matemáticas, uno de los aspectos fundamentales que a menudo pasa desapercibido es el uso correcto de la coma en el lenguaje algebraico. Aunque puede parecer un detalle menor, la coma desempeña un papel crucial en la claridad y precisión de las expresiones matemáticas. Este artículo tiene como objetivo destacar la importancia de este signo de puntuación y proporcionar estrategias para su correcta enseñanza en el aula.
La Coma y su Significado en Álgebra
En el contexto del álgebra, la coma puede tener múltiples funciones, dependiendo del contexto en el que se utilice. Algunas de las funciones más comunes incluyen:
Separación de términos en una expresión: En algunas notaciones, especialmente en álgebra lineal y cálculo, la coma se utiliza para separar diferentes términos o componentes de un vector o una lista. Por ejemplo, en un vector, las comas separan los diferentes componentes del vector.
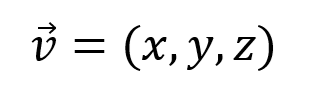
Desambiguación en expresiones verbales: En el lenguaje natural, la coma ayuda a clarificar el significado de las expresiones. Por ejemplo, «una cantidad aumentada en siete, elevado al cuadrado» se escribe algebraicamente de la siguiente forma. En este caso la coma se debe interpretar como un paréntesis.
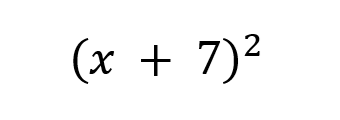
Separación de elementos en conjuntos y listas: En teoría de conjuntos y en la notación de listas, la coma se utiliza para separar los elementos. Por ejemplo, la coma cumple la función de separar los elementos.
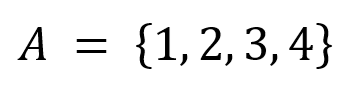
Importancia de la Coma en la Enseñanza
Para los estudiantes, la correcta interpretación de la coma en las expresiones algebraicas es esencial para evitar malentendidos y errores. A continuación, se presentan algunas razones clave por las cuales los profesores de matemáticas deben enfatizar el uso correcto de la coma:
Claridad y Precisión: La coma ayuda a clarificar la estructura de las expresiones algebraicas, lo que facilita su comprensión y análisis. Una expresión clara y bien estructurada permite a los estudiantes identificar fácilmente los diferentes componentes y operaciones.
Prevención de Errores: La incorrecta colocación o la omisión de una coma puede llevar a errores significativos en los cálculos y en la interpretación de las expresiones. Por ejemplo, confundir las siguientes expresiones.
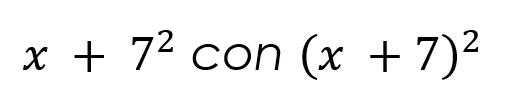
Desarrollo de Habilidades de Comunicación Matemática: Enseñar a los estudiantes a utilizar correctamente la coma en el lenguaje algebraico fomenta el desarrollo de habilidades de comunicación matemática. Esto es crucial para la presentación de soluciones y para la colaboración en trabajos en grupo y proyectos.
Estrategias para Enseñar el Uso Correcto de la Coma
Para asegurar que los estudiantes comprendan y utilicen correctamente la coma en sus expresiones algebraicas, los profesores pueden adoptar las siguientes estrategias:
Explicación y Ejemplificación: Proporcione explicaciones claras y ejemplos específicos que muestren cómo la coma afecta la interpretación de las expresiones algebraicas. Compare y contraste ejemplos correctos e incorrectos.
Práctica Guiada: Diseñe ejercicios que requieran a los estudiantes utilizar la coma en diferentes contextos algebraicos. Revise las respuestas en clase, destacando los errores comunes y corrigiéndolos colectivamente.
Feedback Constante: Proporcione retroalimentación específica sobre el uso de la coma en las tareas y exámenes. Esto ayudará a los estudiantes a comprender sus errores y a mejorar su precisión.
Recursos Visuales: Utilice diagramas y gráficos para ilustrar cómo la coma separa los términos y afecta la estructura de las expresiones. Los recursos visuales pueden hacer que los conceptos abstractos sean más tangibles y comprensibles.
El uso correcto de la coma en el lenguaje algebraico es un detalle fundamental que puede tener un gran impacto en la comprensión y precisión de las expresiones matemáticas. Como profesores de matemáticas, es nuestra responsabilidad asegurarnos de que los estudiantes comprendan la importancia de este signo de puntuación y sepan cómo utilizarlo correctamente. Al enfatizar la claridad, la práctica y la retroalimentación, podemos ayudar a nuestros estudiantes a desarrollar habilidades sólidas en la comunicación matemática y a evitar errores comunes que pueden surgir de una mala interpretación de las expresiones algebraicas.
Atte. Patricio Figueroa M – Profesor de Matemáticas








