El Teorema de los Cuatro Cuadrados es un resultado fundamental en teoría de números que se relaciona con la representación de números enteros como la suma de cuatro cuadrados enteros. Este teorema, que ha intrigado a matemáticos durante siglos, fue demostrado de manera rigurosa por el matemático Joseph-Louis Lagrange en el siglo XVIII.
Lagrange fue un destacado matemático e inventor italo-francés, nacido el 25 de enero de 1736 en Turín, Italia, y fallecido el 10 de abril de 1813 en París, Francia. Su vida y trabajo dejaron una huella perdurable en las matemáticas y la física, y es considerado uno de los más grandes matemáticos de la historia.
Declaración del Teorema:
El teorema establece que cualquier número entero positivo n puede expresarse como la suma de cuatro cuadrados enteros, es decir, números que son cuadrados perfectos. Matemáticamente, esto se expresa de la siguiente manera:
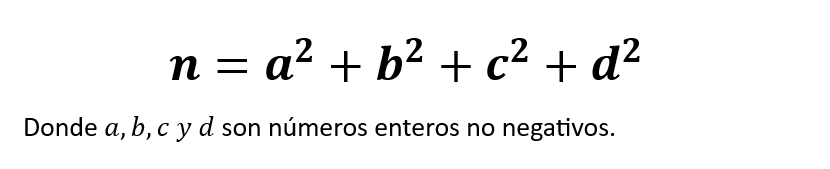
Historia y Significado:
El Teorema de los Cuatro Cuadrados ha intrigado a matemáticos durante siglos y ha sido objeto de investigación y especulación desde la antigüedad. La demostración rigurosa de Lagrange en el siglo XVIII finalmente resolvió este problema fundamental en teoría de números.
Este teorema tiene aplicaciones en diversas áreas de las matemáticas y la física, como la teoría de números, la teoría de grupos y la teoría de formas cuadráticas. Además, ha sido fundamental en la comprensión de las propiedades de los números enteros y ha influido en áreas tan diversas como la teoría de códigos y la criptografía.
Ejemplo:
Un ejemplo simple de este teorema es la representación del número 7:
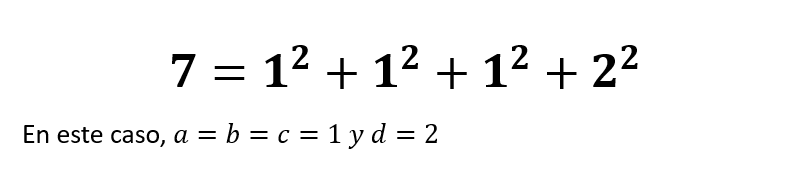
El Teorema de los Cuatro Cuadrados es un resultado importante en teoría de números que demuestra que cualquier número entero positivo puede expresarse como la suma de cuatro cuadrados enteros. Aunque su demostración es compleja, su aplicabilidad y su papel en la comprensión de los números enteros lo convierten en un teorema fundamental en matemáticas.
Para conocer más detalles acerca de este teorema, puede visitar la excelente página web que recomiendo en el siguiente enlace, gaussianos.com
Atte. Patricio Figueroa M – Profesor de Matemáticas







